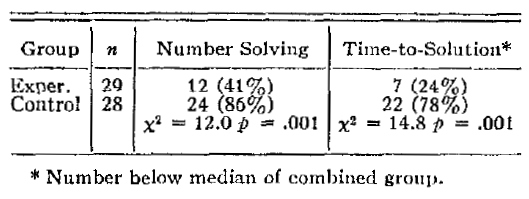Psychology Classics On Amazon

Functional Fixedness As Related To Problem Solving
Landmark article by Robert Adamson confirming Gestalt psychologist Karl Duncker's groundbreaking findings on the inhibiting affect of functional fixedness on problem solving.
The Article in Full
The study of problem solving and thinking has been retarded by the lack of agreed-upon theoretical concepts supported by adequate data from experiments. As a part of a larger program concerned with these matters, some of the more promising hypotheses have been assembled, and preliminary experiments undertaken to repeat the demonstrations upon which these hypotheses rest.
One inviting hypothesis is that problem solving may in some instances be delayed through the "functional fixedness" of solution objects. That is, owing to his previous use of the object in a function dissimilar to that demanded by the present problem, S is inhibited in discovering the appropriate new use of the object. This hypothesis was proposed by Duncker (3), who designed ingenious experiments to support it, but carried the experiments through with but 14 Ss and under poorly specified experimental conditions. It seemed wise, therefore, to repeat some of his experiments both to substantiate his results, if possible, and to ascertain the efficacy of the problems for use in further investigations. The success of Birch and Rabinowitz (1) in demonstrating functional fixedness in a related experiment encouraged us to hope for positive results.
PROCEDURE
Subjects: All Ss taking part in this study were college students from elementary psychology classes. There were 57 Ss, of whom 35 were men, 22 women. Twenty-nine Ss were assigned to the experimental group, 28 to the control group. All Ss were of proximate ages and had been exposed to little experimentation.
Problems: Duncker's "box," "gimlet," and "paperclip" problems were presented to each S in the order named. In the first of these, the box problem, S's task is to mount three candles vertically on a screen, at a height of about 5 ft., using to accomplish this task any of a large number of objects which are lying before S on a table. Among these objects are three pasteboard boxes of varying sixes, five matches, and five thumbtacks, the crucial objects for solution of the problem. The solution is to mount one candle on each box by melting wax on the box and sticking the candle to it, then to tack the boxes to the screen.
The gimlet problem involves suspending three cords from a board attached to an overhead beam. Among the variety of objects available are two screw-hooks and the gimlet itself, the objects from which the cords may be hung.
The paperclip problem consists of first attaching four small black cardboard squares to a large white square, then hanging the large square from an eyelet screwed into the aforementioned beam. Included among the objects lying before S on the table are a number of paperclips. These may be used to attach the small squares to the large one, and one of them, when bent to form a hook, will serve to hang the large square from the eyelet.
DESIGN
The experimental and control groups were given the same problems to solve. For the experimental group, however, at least one of the solution objects was "burdened" with a prior function in each problem. Thus, the candles, matches, and tacks for the box problem were placed in the three boxes before they were given to S. Hence, the boxes had for their initial function that of containing, whereas in their solution function they had to be used as supports or platforms. Similarly the gimlet initially had to be used to start holes for the screw-hooks, and in the paperclip problem, the four black squares had to be attached to the white one with paperclips. Duncker referred to the experimental group as the "after pre-utilization" group.
The control group was given the problems without any pre-utilization. In the case of the box problem, the empty boxes were placed on the table at varying distances from the other crucial solution objects. Holes into which the screwhooks and the gimlet could be screwed were already drilled into the beam in the case of the gimlet problem; the four black squares were stapled to the white one in the paperclip problem. Thus, none of the crucial objects was used with a function prior to its use as a solution object.
Solution scores were taken as one possible measure of functional fixedness, and time to solution constituted another measure. A maximum time of 20 min. was allowed for solution of each of the problems.
RESULTS
Box problem: The results of the box problem, presented in Table 1, confirm Duncker's finding that functional fixedness results from pre-utilization. The performance of the experimental group was markedly inferior to that of the control with respect both to the number of solutions obtained and the time required to reach solution. Prior usage of the boxes as containers inhibited their being used as platforms.
Table 1: Box Problem
The chi-square value comparing the two groups on the time score was obtained by using as a cutting point the median time-to-solution of the combined groups. All cases for which there was no solution were assigned to the above-median category. With 1 df, each of the chi squares was highly significant. Since the direction of the difference was predicted, a one-tail test of significance was employed for both this and the following two problems.
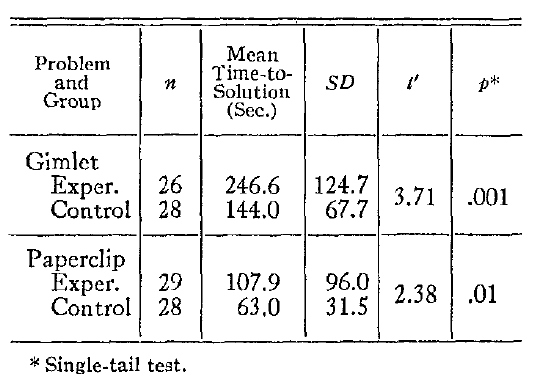
Gimlet problem: Since only three Ss failed to solve this problem, all from the experimental group, the solution score could not demonstrate a difference between the experimental and control groups. Accordingly, only the results from the time measure are given in Table 2. The three Ss failing to reach solution were not considered in the analysis of the data, thus reducing the total n to 54 for this experiment.
Since, as shown in Table 2, the variances for the two groups are not homogeneous, the use of it as a test of significance was inappropriate. Instead, t' was employed. The highly significant difference obtained shows clearly the presence of functional fixedness.
Paperclip problem: The results from the paperclip problem are also shown in Table 2. Since all Ss were able to solve this problem, only time scores are given. As in the first two problems, pre-utilization of the solution objects with a function different from that demanded by the problem resulted in significantly poorer performance by the experimental group.
Table 2: Gimlet & Paperclip Problems
Reliability of individual performance: An analysis was made of the performance of the experimental group to determine whether individual achievement on one of the three problems was significantly related to achievement on either of the other two. Chi square was used to test whether individuals scoring below the median in time-to-solution for one of two problems also showed a significant tendency to score below the median for the other. (Since only 12 of 29 Ss solved the box problem, a median time-to-solution could not be obtained; instead, the distribution was dichotomized in terms of solution or no solution.) A relation significant at the .05 level was found between the box problem and the paperclip problem. Neither of the other chi squares was significant. Clearly, achievement on a single problem involving pre-utilization is not a reliable measure of individual susceptibility to functional fixedness.
DISCUSSION
Duncker's study (3), involving these three experiments, used two measures of performance: number of presolutions, and number of solutions. In the present study, the number of presolutions was discarded as a measure, because it was found to be overly dependent upon the subjective judgment of E. Number of solutions proved to be a satisfactory measure for only the box problem. Since all Ss solved the paperclip problem, and all but three solved the gimlet problem, no difference between the experimental and the control groups could be revealed by this measure. It would appear that the Ss in the present study were more able than those employed by Duncker.
Although the measures previously used by Duncker failed to show functional fixedness in two of the three present experiments, a new measure, time-to-solution, gave positive results in all three experiments. Essentially, then, the present results confirm those obtained by Duncker.
The results of Duncker, of Birch and Rabinowitz, and those obtained in this study afford convincing proof of the existence of functional fixedness. The reality of this phenomenon having been established, two lines of investigation are of immediate interest: (a) determination of those conditions which influence the occurrence of functional fixedness, and (b) exploration of its relation to other kinds of set in problem solving. A study now nearing completion involves both of these lines of experimentation.
SUMMARY
Three of Duncker's experiments on functional fixedness were repeated in this study. Fifty-seven Ss were used, 29 serving as the experimental and 28 as the control group. Both groups were given the "box," "gimlet," and "paperclip" problems in that order. Experimental Ss were given each problem after first having used the solution objects for that problem in a function dissimilar to that demanded for solution. Control Ss were given the problems without such preutilization.
Two measures of performance were used: number of solutions, and time-to-solution. The former measure discriminated between the experimental and control groups on only the box problem; the latter measure gave highly significant differences in the expected direction for all three problems.
Functional fixedness was shown to result from the pre-utilization of solution objects. Duncker's results were confirmed in a study using a larger n and having more carefully specified experimental conditions.
REFERENCES
1. BIRCH, H. G., & RABINOWITZ, H. S. The negative effect of previous experience on productive thinking. J. exp. Psychol., 1951,41, 121-125.
2. COCHRAN, W. G., & Cox, G. M. Experimental design. New York: John Wiley & Sons, 1950.
3. DUNCKER, K. On problem-solving. Psychol. Monogr., 1945,58, No. 5 (Whole No. 270).
Recent Articles
-
The Psychology of Dreams
Apr 23, 24 10:34 AM
Learn all about the psychology of dreams. -
Skill Improvement
Apr 22, 24 08:24 AM
How do you come up with exercises to improve a specific skill? I can only think of two or three exercises at best, but I need more If I want to improve -
Limits of Self Control Improvement
Apr 21, 24 06:00 AM
I’ve been trying to improve my self-control or willpower incrementally, 5 minutes, 20 minutes, 30 minutes, so on and so forth. Is there a ceiling to how
Please help support this website by visiting the All About Psychology Amazon Store to check out an awesome collection of psychology books, gifts and T-shirts.
Know Someone Who Would Love To Read Functional Fixedness As Related To Problem Solving. Share This Page With Them.
Go To The Classic Psychology Journal Articles Page